Contact Spring Calculations

6.4.7 Contact Spring Calculations

One side fixed contact bending spring

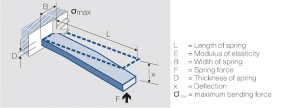
The influence of the dimensions can be illustrated best by using the single side fixed beam model Figure 1 . For small deflections the following equation is valid:

$F = \frac{3 \cdot E \cdot J}{L^3} $

where J is the momentum of inertia of the rectangular cross section of the beam

$J = \frac{B \cdot D^3}{12}$

For springs with a circular cross-sectional area the momentum of inertia is

$J=\pi D^4/64$

$D= Durchmesser$

To avoid plastic deformation of the spring the max bending force σ_max cannot be exceeded

$\sigma_{max} = \frac{3 \cdot E \cdot D}{2L^2}\cdot_{max}$

The stress limit is defined through the fatigue limit and the 0.2% elongation limit resp.

$\times_{max} = \frac{2 \cdot L^2}{3 \cdot D \cdot E}R_{p0,2}$

and/or

$F_{max} = \frac{B \cdot D^2}{6L}R_{p0,2}$

Special Spring Shapes

• Triangular spring

Deflection

$ \times = \frac{F}{2 \cdot E \cdot J}L^3$




$= \frac{6 \cdot F}{E \cdot B}\cdot \frac{L^3}{D^3}$


Max. bending force

$\sigma_{max}= \frac{18 \cdot F \cdot L}{B \cdot D^2}$

• Trapezoidal spring

Deflection

$ \times = \frac{F}{(2 + B_{min} /B_{max})}\times \frac{L^3}{E \cdot J}$




$\times= \frac{12 \cdot F}{(2 + B_{min} /B_{max})}\cdot \frac{L^3}{E \cdot B \cdot D^3}$


Max. bending force

$\sigma_{max}= \frac{18 \cdot F \cdot L}{(2 + B_{min} /B_{max}) \cdot B_{max} \cdot D^2 }$

References

References