Difference between revisions of "Contact Spring Calculations"
From Electrical Contacts
(→Contact Spring Calculations) |
Doduco Admin (talk | contribs) m (Reverted edits by Doduco Redaktion (talk) to last revision by STZAdmin) (Tag: Rollback) |
||
| Line 1: | Line 1: | ||
| − | + | ===<!--6.4.7-->Contact Spring Calculations=== | |
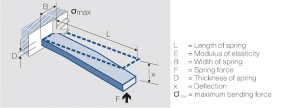
| − | + | <figure id="fig:Oneside_fixed_contact_bending_spring"> | |
| − | + | [[File:One side fixed contact bending spring.jpg|right|thumb|One side fixed contact bending spring]] | |
| − | + | </figure> | |
| − | + | The influence of the dimensions can be illustrated best by using the single side fixed beam model <xr id="fig:Oneside_fixed_contact_bending_spring"/><!--(Fig. 6.20)-->. For small deflections the following equation is valid: | |
| − | + | :$F = \frac{3 \cdot E \cdot J}{L^3} $ | |
| − | |||
| − | |||
| − | | | ||
| − | | | ||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | where J is the momentum of inertia of the rectangular cross section of the beam | |
| − | + | :$J = \frac{B \cdot D^3}{12}$ | |
| − | + | ||
| − | + | For springs with a circular cross-sectional area the momentum of inertia is | |
| − | + | :$J=\pi D^4/64$ | |
| − | + | :$D= Durchmesser$ | |
| − | + | ||
| − | + | To avoid plastic deformation of the spring the max bending force σ<sub>max</sub> cannot be exceeded | |
| − | + | :$\sigma_{max} = \frac{3 \cdot E \cdot D}{2L^2}\cdot_{max}$ | |
| − | + | ||
| − | + | The stress limit is defined through the fatigue limit and the 0.2% elongation limit resp. | |
| − | | | + | :$\times_{max} = \frac{2 \cdot L^2}{3 \cdot D \cdot E}R_{p0,2}$ |
| − | + | ||
| + | <br />and/or<br /> | ||
| + | :$F_{max} = \frac{B \cdot D^2}{6L}R_{p0,2}$ | ||
| + | |||
| + | |||
| + | <li>'''Special Spring Shapes'''</li> | ||
| + | <ul> | ||
| + | <li>'''Triangular spring'''</li> | ||
| + | |||
| + | Deflection | ||
| + | :$ \times = \frac{F}{2 \cdot E \cdot J}L^3$ | ||
| + | |||
| + | |||
| + | :$= \frac{6 \cdot F}{E \cdot B}\cdot \frac{L^3}{D^3}$ | ||
| + | |||
| + | |||
| + | Max. bending force | ||
| + | :$\sigma_{max}= \frac{18 \cdot F \cdot L}{B \cdot D^2}$ | ||
| + | |||
| + | <li>'''Trapezoidal spring'''</li> | ||
| + | |||
| + | Deflection | ||
| + | :$ \times = \frac{F}{(2 + B_{min} /B_{max})}\times \frac{L^3}{E \cdot J}$ | ||
| + | |||
| + | |||
| + | :$\times= \frac{12 \cdot F}{(2 + B_{min} /B_{max})}\cdot \frac{L^3}{E \cdot B \cdot D^3}$ | ||
| + | |||
| + | |||
| + | Max. bending force | ||
| + | :$\sigma_{max}= \frac{18 \cdot F \cdot L}{(2 + B_{min} /B_{max}) \cdot B_{max} \cdot D^2 }$ | ||
| + | </ul> | ||
| + | |||
| + | |||
| + | ==References== | ||
| + | [[Application Tables and Guideline Data for Use of Electrical Contact Design#References|References]] | ||
| + | |||
| + | [[de:Berechnung_von_Kontaktfedern]] | ||
Revision as of 08:55, 11 January 2023
Contact Spring Calculations
The influence of the dimensions can be illustrated best by using the single side fixed beam model Figure 1. For small deflections the following equation is valid:
- $F = \frac{3 \cdot E \cdot J}{L^3} $
where J is the momentum of inertia of the rectangular cross section of the beam
- $J = \frac{B \cdot D^3}{12}$
For springs with a circular cross-sectional area the momentum of inertia is
- $J=\pi D^4/64$
- $D= Durchmesser$
To avoid plastic deformation of the spring the max bending force σmax cannot be exceeded
- $\sigma_{max} = \frac{3 \cdot E \cdot D}{2L^2}\cdot_{max}$
The stress limit is defined through the fatigue limit and the 0.2% elongation limit resp.
- $\times_{max} = \frac{2 \cdot L^2}{3 \cdot D \cdot E}R_{p0,2}$
and/or
- $F_{max} = \frac{B \cdot D^2}{6L}R_{p0,2}$
- Triangular spring
- $ \times = \frac{F}{2 \cdot E \cdot J}L^3$
- $= \frac{6 \cdot F}{E \cdot B}\cdot \frac{L^3}{D^3}$
- $\sigma_{max}= \frac{18 \cdot F \cdot L}{B \cdot D^2}$
- Trapezoidal spring
- $ \times = \frac{F}{(2 + B_{min} /B_{max})}\times \frac{L^3}{E \cdot J}$
- $\times= \frac{12 \cdot F}{(2 + B_{min} /B_{max})}\cdot \frac{L^3}{E \cdot B \cdot D^3}$
- $\sigma_{max}= \frac{18 \cdot F \cdot L}{(2 + B_{min} /B_{max}) \cdot B_{max} \cdot D^2 }$
Deflection
Max. bending force
Deflection
Max. bending force