Difference between revisions of "Berechnung von Kontaktfedern"

From Electrical Contacts
Jump to: navigation, search
(→‎Berechnung von Kontaktfedern)
 
Line 1: Line 1:
 
===<!--6.4.7-->Berechnung von Kontaktfedern===
 
===<!--6.4.7-->Berechnung von Kontaktfedern===
 
<figure id="fig:Oneside_fixed_contact_bending_spring">
 
<figure id="fig:Oneside_fixed_contact_bending_spring">
−
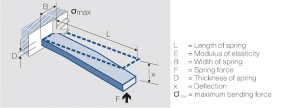
[[File:One side fixed contact bending spring.jpg|right|thumb|Einseitig eingespannte Biegefeder]]
+
[[File:One side fixed contact bending spring.jpg|right|thumb|Figure 1: Einseitig eingespannte Biegefeder]]
 
</figure>
 
</figure>
 
Der Einfluss der Abmessungen lässt sich am einfachsten am einseitig
 
Der Einfluss der Abmessungen lässt sich am einfachsten am einseitig

Latest revision as of 08:39, 4 January 2023

Berechnung von Kontaktfedern

Figure 1: Einseitig eingespannte Biegefeder

Der Einfluss der Abmessungen lässt sich am einfachsten am einseitig eingespannten Biegebalken erkennen (Figure 1). Unter der Voraussetzung kleiner Auslenkungen ergibt sich folgende Beziehung:

F = \frac{3 \cdot E \cdot J}{L^3}

wobei das Trägheitsmoment des rechteckigen Balkenquerschnitts ist

J = \frac{B \cdot D^3}{12}

Für Federn mit kreisförmigem Querschnitt gilt

J=\pi D^4/64
D= Durchmesser

Um eine plastische Verformung der Feder zu vermeiden, darf die Biegespannung Fmax nicht überschritten werden.

\sigma_{max} = \frac{3 \cdot E \cdot D}{2L^2}\cdot_{max}

Die Grenzbelastung wird durch die Federbiegegrenze bzw. die 0,2% - Dehngrenze (Rp0,2) bestimmt

\times_{max} = \frac{2 \cdot L^2}{3 \cdot D \cdot E}R_{p0,2}


bzw.

F_{max} = \frac{B \cdot D^2}{6L}R_{p0,2}


  • Spezielle Federformen
    • Dreieckfeder

      • Auslenkung

      \times = \frac{F}{2 \cdot E \cdot J}L^3


      = \frac{6 \cdot F}{E \cdot B}\cdot \frac{L^3}{D^3}


      max. Biegespannung

      \sigma_{max}= \frac{18 \cdot F \cdot L}{B \cdot D^2}
    • Trapezfeder

      • Auslenkung

      \times = \frac{F}{(2 + B_{min} /B_{max})}\times \frac{L^3}{E \cdot J}


      \times= \frac{12 \cdot F}{(2 + B_{min} /B_{max})}\cdot \frac{L^3}{E \cdot B \cdot D^3}


      max. Biegespannung

      \sigma_{max}= \frac{18 \cdot F \cdot L}{(2 + B_{min} /B_{max}) \cdot B_{max} \cdot D^2 }

    Referenzen

    Referenzen

    Retrieved from "https://www.electrical-contacts-wiki.com/index.php?title=Berechnung_von_Kontaktfedern&oldid=5103"