Difference between revisions of "Contact Spring Calculations"
From Electrical Contacts
(→6.4.7 Contact Spring Calculations) |
(→6.4.7 Contact Spring Calculations) |
||
| Line 43: | Line 43: | ||
| − | :<math>\times= \frac{12 \cdot F}{(2 + B_{min} /B_{max})}\ | + | :<math>\times= \frac{12 \cdot F}{(2 + B_{min} /B_{max})}\cdot \frac{L^3}{E \cdot B \cdot D^3}</math> |
Revision as of 13:48, 30 April 2014
6.4.7 Contact Spring Calculations
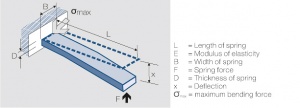
The influence of the dimensions can be illustrated best by using the single side fixed beam model Figure 1 (Fig. 6.20). For small deflections the following equation is valid:
where J is the momentum of inertia of the rectangular cross section of the beam
For springs with a circular cross-sectional area the momentum of inertia is
To avoid plastic deformation of the spring the max bending force σmax cannot be exceeded
The stress limit is defined through the fatigue limit and the 0.2% elongation limit resp.
and/or
- Triangular spring
- Trapezoidal spring
Deflection
Max. bending force
Deflection
Max. bending force