Difference between revisions of "Contact Spring Calculations"
From Electrical Contacts
Doduco Admin (talk | contribs) (Blanked the page) (Tag: Blanking) |
|||
| (12 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| + | ===6.4.7 Contact Spring Calculations=== | ||
| + | <figure id="fig:Oneside_fixed_contact_bending_spring"> | ||
| + | [[File:One side fixed contact bending spring.jpg|right|thumb|One side fixed contact bending spring]] | ||
| + | </figure> | ||
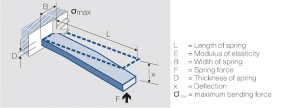
| + | The influence of the dimensions can be illustrated best by using the single side fixed beam model <xr id="fig:Oneside_fixed_contact_bending_spring"/> (Fig. 6.20). For small deflections the following equation is valid: | ||
| + | :$F = \frac{3 \cdot E \cdot J}{L^3} $ | ||
| + | where J is the momentum of inertia of the rectangular cross section of the beam | ||
| + | :$J = \frac{B \cdot D^3}{12}$ | ||
| + | |||
| + | For springs with a circular cross-sectional area the momentum of inertia is | ||
| + | :$J=\pi D^4/64$ | ||
| + | :$D= Durchmesser$ | ||
| + | |||
| + | To avoid plastic deformation of the spring the max bending force σ<sub>max</sub> cannot be exceeded | ||
| + | :$\sigma_{max} = \frac{3 \cdot E \cdot D}{2L^2}\cdot_{max}$ | ||
| + | |||
| + | The stress limit is defined through the fatigue limit and the 0.2% elongation limit resp. | ||
| + | :$\times_{max} = \frac{2 \cdot L^2}{3 \cdot D \cdot E}R_{p0,2}$ | ||
| + | |||
| + | <br />and/or<br /> | ||
| + | :$F_{max} = \frac{B \cdot D^2}{6L}R_{p0,2}$ | ||
| + | |||
| + | |||
| + | <li>'''Special Spring Shapes'''</li> | ||
| + | <ul> | ||
| + | <li>'''Triangular spring'''</li> | ||
| + | |||
| + | Deflection | ||
| + | :$ \times = \frac{F}{2 \cdot E \cdot J}L^3$ | ||
| + | |||
| + | |||
| + | :$= \frac{6 \cdot F}{E \cdot B}\cdot \frac{L^3}{D^3}$ | ||
| + | |||
| + | |||
| + | Max. bending force | ||
| + | :$\sigma_{max}= \frac{18 \cdot F \cdot L}{B \cdot D^2}$ | ||
| + | |||
| + | <li>'''Trapezoidal spring'''</li> | ||
| + | |||
| + | Deflection | ||
| + | :$ \times = \frac{F}{(2 + B_{min} /B_{max})}\times \frac{L^3}{E \cdot J}$ | ||
| + | |||
| + | |||
| + | :$\times= \frac{12 \cdot F}{(2 + B_{min} /B_{max})}\cdot \frac{L^3}{E \cdot B \cdot D^3}$ | ||
| + | |||
| + | |||
| + | Max. bending force | ||
| + | :$\sigma_{max}= \frac{18 \cdot F \cdot L}{(2 + B_{min} /B_{max}) \cdot B_{max} \cdot D^2 }$ | ||
| + | </ul> | ||
| + | |||
| + | ==References== | ||
| + | [[Application Tables and Guideline Data for Use of Electrical Contact Design#References|References]] | ||
Revision as of 12:02, 14 May 2014
6.4.7 Contact Spring Calculations
The influence of the dimensions can be illustrated best by using the single side fixed beam model Figure 1 (Fig. 6.20). For small deflections the following equation is valid:
- $F = \frac{3 \cdot E \cdot J}{L^3} $
where J is the momentum of inertia of the rectangular cross section of the beam
- $J = \frac{B \cdot D^3}{12}$
For springs with a circular cross-sectional area the momentum of inertia is
- $J=\pi D^4/64$
- $D= Durchmesser$
To avoid plastic deformation of the spring the max bending force σmax cannot be exceeded
- $\sigma_{max} = \frac{3 \cdot E \cdot D}{2L^2}\cdot_{max}$
The stress limit is defined through the fatigue limit and the 0.2% elongation limit resp.
- $\times_{max} = \frac{2 \cdot L^2}{3 \cdot D \cdot E}R_{p0,2}$
and/or
- $F_{max} = \frac{B \cdot D^2}{6L}R_{p0,2}$
- Triangular spring
- $ \times = \frac{F}{2 \cdot E \cdot J}L^3$
- $= \frac{6 \cdot F}{E \cdot B}\cdot \frac{L^3}{D^3}$
- $\sigma_{max}= \frac{18 \cdot F \cdot L}{B \cdot D^2}$
- Trapezoidal spring
- $ \times = \frac{F}{(2 + B_{min} /B_{max})}\times \frac{L^3}{E \cdot J}$
- $\times= \frac{12 \cdot F}{(2 + B_{min} /B_{max})}\cdot \frac{L^3}{E \cdot B \cdot D^3}$
- $\sigma_{max}= \frac{18 \cdot F \cdot L}{(2 + B_{min} /B_{max}) \cdot B_{max} \cdot D^2 }$
Deflection
Max. bending force
Deflection
Max. bending force